Some while ago (during or not too long after my college years), I found the following page in a collection of M.C. Escher’s notebooks, describing overlapping motifs on tiles, which, when arranged in various rotations, result in woven designs.

Using Adobe Illustrator at the time, I experimented with some tiles of my own. Initially I made some squares, but eventually designed some hexagonal tiles as well.

Recently I resurrected the square designs to start working with these by programming because it is tedious to do it by hand. Using the Processing language, I made two tiles, an “over” version and an “under” version.

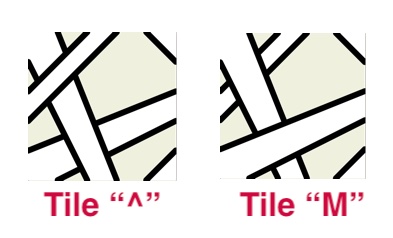
Why they’re labeled “^” and “M” I’ll get to in a moment. Here’s a random tiling with both tiles, in various rotations.

Once I could draw the tiles, I wanted to create more controlled layouts, using tile substitution.

In order to define substitution rules, I needed an alphabet to describe both the over and under tiles, in the various rotations. Escher used “A” and “B” with under bars to represent the “over-underness”, and then rotated the letters. I noodled a bit with Unicode characters that had rotations, thinking “T” and “E” (as in T and E modules) would be nice choices for reasons that maybe one other person I know might understand.

Being lazy, I preferred to use ASCII characters, and I settled on the following alphabet to represent the rotations of the over and under tiles:

^ > v < 
M 3 W E

Having an alphabet, I could now represent substitutions of one tile for a quad of 4 tiles, like this:

M -> < E
     3 >

or, more succinctly as

M -> <E|3>

Now, given a ruleset like

^ -> EE|33
> -> MW|WM
v -> 33|EE
< -> WM|MW
M -> <E|3>
3 -> ^v|M^
W -> 3>|<E
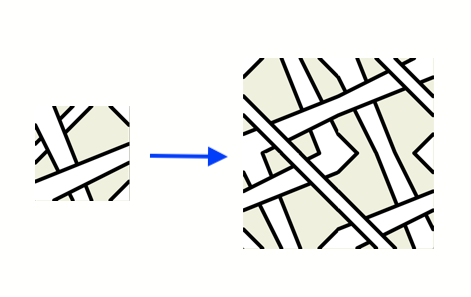
E -> v^|Mv

Starting with an axiom of ‘^’ and doing 3 iterations of substitutions (replace the axiom, then replace each of those 4 squares, then replace each of those 16 squares…) you get a somewhat more orderly design.

Which is represented by

E E 3 3 E E 3 3 3 3 E E 3 3 E E E E 3 3 E E 3 3 3 3 E E 3 3 E E
3 3 E E 3 3 E E E E 3 3 E E 3 3 3 3 E E 3 3 E E E E 3 3 E E 3 3
< E E E < E E E < E 3 3 < E 3 3 < E E E < E E E < E 3 3 < E 3 3
3 > 3 3 3 > 3 3 3 > E E 3 > E E 3 > 3 3 3 > 3 3 3 > E E 3 > E E
3 3 E E 3 3 E E E E 3 3 E E 3 3 3 3 E E 3 3 E E E E 3 3 E E 3 3
E E 3 3 E E 3 3 3 3 E E 3 3 E E E E 3 3 E E 3 3 3 3 E E 3 3 E E
< E 3 3 < E 3 3 < E E E < E E E < E 3 3 < E 3 3 < E E E < E E E
3 > E E 3 > E E 3 > 3 3 3 > 3 3 3 > E E 3 > E E 3 > 3 3 3 > 3 3
3 > < E 3 3 E E E E 3 3 E E 3 3 3 > < E 3 3 E E E E 3 3 E E 3 3
< E 3 > E E 3 3 3 3 E E 3 3 E E < E 3 > E E 3 3 3 3 E E 3 3 E E
< E 3 > < E 3 3 < E E E < E E E < E 3 > < E 3 3 < E E E < E E E
3 > < E 3 > E E 3 > 3 3 3 > 3 3 3 > < E 3 > E E 3 > 3 3 3 > 3 3
E E 3 3 < E 3 > 3 3 E E 3 3 E E E E 3 3 < E 3 > 3 3 E E 3 3 E E
3 3 E E 3 > < E E E 3 3 E E 3 3 3 3 E E 3 > < E E E 3 3 E E 3 3
< E E E 3 > < E < E 3 3 < E 3 3 < E E E 3 > < E < E 3 3 < E 3 3
3 > 3 3 < E 3 > 3 > E E 3 > E E 3 > 3 3 < E 3 > 3 > E E 3 > E E
3 3 E E 3 3 E E E E 3 3 E E 3 3 3 3 E E 3 3 E E E E 3 3 E E 3 3
E E 3 3 E E 3 3 3 3 E E 3 3 E E E E 3 3 E E 3 3 3 3 E E 3 3 E E
< E 3 3 < E 3 3 < E E E < E E E < E 3 3 < E 3 3 < E E E < E E E
3 > E E 3 > E E 3 > 3 3 3 > 3 3 3 > E E 3 > E E 3 > 3 3 3 > 3 3
E E 3 3 E E 3 3 3 3 E E 3 3 E E E E 3 3 E E 3 3 3 3 E E 3 3 E E
3 3 E E 3 3 E E E E 3 3 E E 3 3 3 3 E E 3 3 E E E E 3 3 E E 3 3
< E E E < E E E < E 3 3 < E 3 3 < E E E < E E E < E 3 3 < E 3 3
3 > 3 3 3 > 3 3 3 > E E 3 > E E 3 > 3 3 3 > 3 3 3 > E E 3 > E E
3 > < E 3 3 E E 3 3 E E 3 3 E E 3 > < E 3 3 E E 3 3 E E 3 3 E E
< E 3 > E E 3 3 E E 3 3 E E 3 3 < E 3 > E E 3 3 E E 3 3 E E 3 3
< E 3 > < E 3 3 < E 3 3 < E 3 3 < E 3 > < E 3 3 < E 3 3 < E 3 3
3 > < E 3 > E E 3 > E E 3 > E E 3 > < E 3 > E E 3 > E E 3 > E E
E E 3 3 < E 3 > E E 3 3 E E 3 3 E E 3 3 < E 3 > E E 3 3 E E 3 3
3 3 E E 3 > < E 3 3 E E 3 3 E E 3 3 E E 3 > < E 3 3 E E 3 3 E E
< E E E 3 > < E < E E E < E E E < E E E 3 > < E < E E E < E E E
3 > 3 3 < E 3 > 3 > 3 3 3 > 3 3 3 > 3 3 < E 3 > 3 > 3 3 3 > 3 3